Source on Github
隐藏图片

Euler Disk 与刚体的纯滚动

  1. 运动微分方程
    1. 绝对坐标系中的运动微分方程
    2. 动坐标系中的运动微分方程
  2. 接触点的几何关系
    1. Euler 盘
    2. 三轴椭球
    3. 轮胎面
  3. 数值求解及可视化
  4. 参考文献

Euler 盘是一个很有意思的教学玩具, 它大概在上世纪九十年代被发明 (命名为 Euler 盘是为了纪念 Euler, 有条件的读者可以查看维基百科), 随后变成了一个较为流行的教学工具. Euler 盘是一个较重的, 扁的圆柱形的铁盘, 另外还有一个光滑的镜面, 使 Euler 盘可以在镜面上旋转. 不同于一个硬币只能在桌子上旋转几秒钟, 一个精心制作的 Euler 盘甚至能旋转 8 分钟, 可参看这个视频.

下面我们将用理论力学的知识对 Euler 盘进行动力学建模, 并使用 Mathematica 求解微分方程, 可视化其运动.

由于 Euler 盘与镜面都是比较光滑的, 在建模时很自然地假设接触点的速度是水平的, 即接触点可以滑动. 然而在文献 Petrie etc.(2002) 中的实验发现, 接触点至少在前期重心位置较高的时候没有滑动, 而是作纯滚动. 因此我们也将采用纯滚动这个假设. 如果读者想参考纯滑动的模型, 可参见我的手写稿 Euler Disk. 考虑这样一个纯滚动的特例的难度, 与考虑任意刚体在水平面的纯滚动问题的难度没有太大区别, 因此我们将先考虑后者, 而后再特例化, 回到我们的模型.

运动微分方程

我们假设读者已经熟悉了刚体动力学的知识, 包括惯性张量, 角速度, 角动量, Euler 角等概念以及它们之间的联系. 这些知识可以在国内的任一本高等动力学教材中找到, 如果读者想看较为数学化的阐述, 可参考 Arnold 的经典教材: 经典力学的数学方法, 也可参看我的读书笔记: 刚体动力学.

一般地, 刚体的运动微分方程在可建立在动系中, 也可建立在绝对坐标系中. 动系中的方程阶次更低, 对于动力学的定性分析更为方便; 虽然绝对坐标系的方程的阶次高, 但其坐标表述较为直观, 也可以直接使用这些坐标得到刚体运动的全部信息. 我们将对这两种建模方式都作介绍.

首先我们引入坐标系并介绍记号. 令 \(oxyz\) 为绝对直角坐标系, \(\hat{o}\hat{x}\hat{y}\hat{z}\) 为从 \(oxyz\) 平移到刚体质心的坐标系, \(OXYZ\) 与刚体固连, 由 \(\hat{o}\hat{x}\hat{y}\hat{z}\) 旋转得到. 见下面的图:

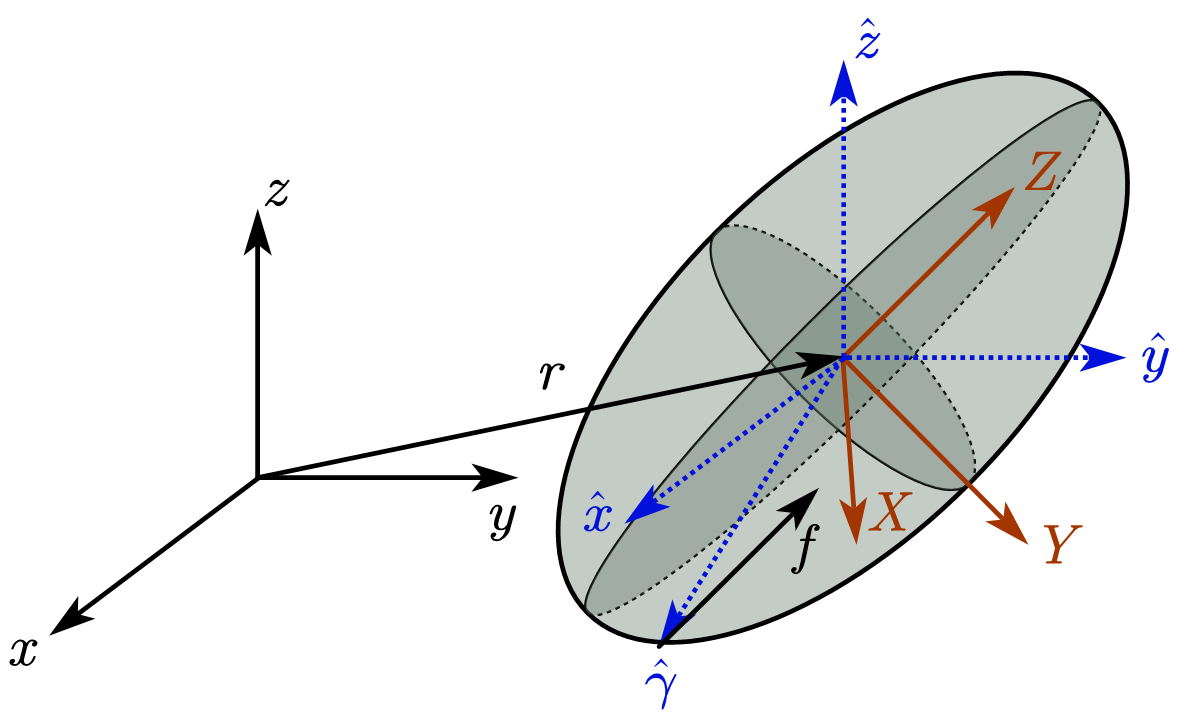
刚体滚动的坐标系统

记号:

  • \(O\) 所在的质心矢径为 \(r\);

  • 大写字母 \(Q\) 表示一个起点为 \(r\) 的矢量在 \(OXYZ\) 中的三个分量;

  • 相应小写字母 \(\hat{q}\) 表示该矢量在 \(\hat{o}\hat{x}\hat{y}\hat{z}\) 中的三个分量;

  • 从 \(\hat{o}\hat{x}\hat{y}\hat{z}\) 到 \(OXYZ\) 的旋转矩阵为 \(A_t\), 即有 \(\hat{q}=A_t Q\);

  • 不加 hat 的小写字母表示在 \(oxyz\) 中的矢量;

  • 接触点矢径为 \(\hat{\gamma}\);

  • 水平面在接触点对刚体的约束反力为 \(f\) (包含支撑力与静摩擦力);

  • 刚体质量为 \(m\), 重力加速度为 \(g\);

  • 刚体在 \(OXYZ\) 下的惯性张量为 \(I\), \(I\) 为对角矩阵, 三个对角元素分别为 \(I_1,I_2,I_3\);

  • 欧拉角采用 \(z-x-z\) 方式旋转, 三个角度分别为 \(\phi,\theta,\psi\);

  • 刚体在 \(OXYZ\) 中的角速度为 \(\Omega\);

  • 水平面的单位法向量记为 \(n=(0,0,1)^T\);

  • 当 \(oxyz\) 中的矢量进行平移时无关紧要, 那么我们就不区分 \(\hat{o}\hat{x}\hat{y}\hat{z}\) 与 \(oxyz\); 例如, 根据上面的约定, 对于 约束反力 \(f\) 在 \(OXYZ\) 中的投影 \(F\), 我们有 \(F=A_t^{-1}f\).

⚠ Note

我们由刚体动力学的知识知道, \(\hat{o}\hat{x}\hat{y}\hat{z}\) 中的矢量如果在刚体坐标系中是静止的, 那么 \(\hat{p}\) 的导数满足:

\[ \dot{\hat{p}}=[\omega,\hat{p}], \]

其中 \([\dcot,\dot]\) 表示三维空间中的矢量积. 一般地, 对于 \(\hat{p}=A_t P\), 我们有:

\[ \frac{d}{dt}A_tP=A_t[\Omega,P]+A_t\dot{P}. \]

绝对坐标系中的运动微分方程

如上图所示, 刚体仅收到重力 \(mgn\) 与约束反力 \(f\), 那么由质心运动定理, 我们有:

\[ m\ddot{r}=-mgn+f . \]

在坐标系 \(OXYZ\) 中, 刚体的动量矩为 \(I\Omega\), 那么动量矩在 \(oxyz\) 中的投影即 \(A_t I\Omega\). 那么根据动量矩定理, 我们有:

\[\frac{d}{dt}\big(A_t I\Omega\big)=[\hat{\gamma},f] .\]

再根据刚体的接触点速度为 \(0\), 那么我们有

\[ \dot{r}+[\omega,\hat{\gamma}]=0. \]

联立方程 (3), (4), 和 (5), 并消去 \(f\) 与 \(\ddot{r}\), 我们得到:

\[ \frac{d}{dt}\big(A_t I\Omega\big)=[\hat{\gamma},mgn-m\frac{d}{dt}[\omega,\hat{\gamma}]] . \]

注意到, 上式的左边可进一步写成如下形式:

\[ \frac{d}{dt}\big(A_t I\Omega\big)=\dot{A_t}I\Omega+A_t I\dot{\Omega}=A_t\big([\Omega,I\Omega]+I\dot{\Omega}\big). \]

那么我们最终有:

\[ A_t\big([\Omega,I\Omega]+I\dot{\Omega}\big)=[\hat{\gamma},mgn-m\frac{d}{dt}[\omega,\hat{\gamma}]] . \]

一般地, 可以将旋转矩阵 \(A_t\) 用三个坐标表示, 通常地是 Euler 角, 但也可以采用单位四元数, 这样, 矩阵 \(A_t\), \(\omega\), \(\Omega\) 都可由这些坐标及其导数所表出. 这里, 我们给出用 Euler 角所表示的这些公式:

\[ A_t= \begin{pmatrix} \cos\phi\cos\psi-\cos\theta\sin\phi\sin\psi&-\cos\theta\cos\psi\sin\phi-\cos\phi\sin\psi&\sin\phi\sin\psi\\ \cos\psi\sin\phi+\cos\theta\cos\phi\sin\psi&\cos\phi\cos\theta\cos\psi-\sin\phi\sin\psi& -\cos\phi\sin\theta \\ \sin\theta\sin\psi&\cos\psi\sin\theta & \cos\theta \\ \end{pmatrix}. \]
\[ \Omega=\begin{pmatrix} \dot{\phi}\sin\theta\sin\psi+\dot{\theta}\cos\psi\\ \notag \dot{\phi}\sin\theta\cos\psi-\dot{\theta}\sin\psi\\ \dot{\psi}+\dot{\phi}\cos\theta\\ \notag \end{pmatrix} \]
\[ \omega=A_t\Omega=\begin{pmatrix} \dot{\theta}\cos\phi+\dot{\psi}\sin\theta\sin\phi\\ \dot{\theta}\sin\phi-\dot{\psi}\sin\theta\cos\phi\\ \dot{\phi}+\dot{\psi}\cos\theta\\ \end{pmatrix} \]

这样, 方程 (8) 中的所有除 \(\hat{\gamma}\) 的量均由 Euler 角及其导数表出了. \(\hat{\gamma}\) 的形式与刚体的几何形状有关, 我们在后面考虑.

动坐标系中的运动微分方程

将方程中的 (8) 中的 \(n,\omega,\hat{\gamma}\) 均用 \(A_tN,A_t\Omega,A_t\Gamma\) 表出. 由于我们有:

\[ \frac{d}{dt}[\omega,\hat{\gamma}]=\frac{d}{dt}A_t[\Omega,\Gamma]=A_t[\Omega,[\Omega,\Gamma]]+A_t\frac{d}{dt}[\Omega,\Gamma]. \]

代入到 (8) 中, 并两边同时左乘 \(A_t^{-1}\) 我们得到:

\[ [\Omega,I\Omega]+I\dot{\Omega}=[\Gamma,mgN-m[\Omega,[\Omega,\Gamma]]-m\frac{d}{dt}[\Omega,\Gamma]]. \]

然而, 上述方程中的 \(N\) 在旋转坐标系 \(OXYZ\) 中不再是常量, 那么我们需要也将其写成微分方程, 我们有:

\[ 0=\frac{d}{dt}(A_tN)=A_t[\Omega,N]+A_t \dot{N}. \]

故我们有

\[ \dot{N}+[\Omega,N]=0. \]

方程 (11) 与方程 (13) 构成了动系下的微分方程, 其状态变量为 \(\Omega,N\). 然而方程中还是有一个量未知, 即 \(\Gamma\), 一般地, 我们将其写成是 \(N\) 的函数. 这是由于在 \(OXYZ\) 中, 一个严格凸刚体的内法线方向总是可以唯一地确定这个刚体上的一个点.

如果要从方程 (11) 与方程 (13) 求得刚体的绝对运动, 还需要如下两步. 第一步是利用方程 (9) 求得 Euler 角的变化; 第二步是利用方程 (5) 求得质心的运动轨迹.

接触点的几何关系

在上一节的两种微分方程中, 均有一个量是未知的, 即接触点矢径 \(\hat{\gamma}\) 关于 Euler 角的函数, 还有在刚体中给定一个内法线方向, 需要唯一地确定一个点 \(\Gamma\), 这个点的内法线即是我们之前给定的. 实际上, 只要知道了函数 \(\Gamma(N)\), 那么我们立即有:

\[ \hat{\gamma}=A_t\Gamma(A_t^{-1}n). \]

利用上面的公式, 就可以用 Euler 角表示 \(\hat{\gamma}\). 因此, 如果要求得 \(\hat{\gamma}\) 关于 Euler 角的显式表达式, 我们一般有两种方式, 第一种是直接利用几何关系求得 \(\hat{\gamma}\), 对于形状比较简单的刚体, 这是有可能实现的; 第二种即是先求 \(\Gamma(N)\), 再利用方程 (14) 算出 \(\hat{\gamma}\).

下面我们给出三个例子, 有兴趣的读者可以尝试计算我们所给出的公式.

Euler 盘

假设 Euler 盘在 \(OXYZ\) 中是这样的圆柱体:

\[ U=\{(X,Y,Z): X^2+Y^2\leq R, |Z|\leq d \} \]

其中 \(R,d>0\) 都是常数. 假设接触点在圆柱体的下表面. 那么, 我们实际上有:

\[ \hat{\gamma}=(R\cos\theta\sin\phi,-R\cos\theta\cos\phi,-R\sin\theta)-dA_t N. \] \[ \Gamma(N)=-\frac{R}{\sqrt{N_1^2+N_2^2}}(N_1,N_2,0)-(0,0,d). \]

三轴椭球

假设三轴椭球在 \(OXYZ\) 中由如下区域给出:

\[ U=\{(X,Y,Z): \frac{X^2}{a^2}+\frac{Y^2}{b^2}+\frac{Z^2}{c^2}\leq1 \} \]

那么我们有:

\[ \Gamma(N)=-(\frac {a^2 N_ 1} {\sqrt {a^2 N_ 1^2 + b^2 N_ 2^2 + c^2 N_ 3^2}},\frac {b^2 N_ 2} {\sqrt {a^2 N_ 1^2 + b^2 N_ 2^2 + c^2 N_ 3^2}},\frac {c^2 N_ 3} {\sqrt {a^2 N_ 1^2 + b^2 N_ 2^2 + c^2 N_ 3^2}}). \]

轮胎面

轮胎面的参数化为:

\[ f(\xi,\eta)=((R+r\cos\eta)\cos\xi,(R+r\cos\eta)\sin\xi,\sin\eta), \]

其中 \(R>r\).

那么我们有

\[ \hat{\gamma}=\left( \begin{array}{c} R \cos (\theta ) \sin (\phi ) \\ -R \cos (\theta ) \cos (\phi ) \\ -r-R \sin (\theta ) \\ \end{array} \right) \]

数值求解及可视化

由于在动坐标系中求解不利于可视化, 我们仅在绝对坐标系下求解方程. 从 \(\hat{\gamma}\) 的计算方式以及表达式, 实际上 Euler 盘的运动与轮胎面的运动十分类似, 下面我们考虑这两个例子.

有许多数值软件或程序包可以求解微分方程, 由于方程的表达式都十分复杂, 我们采用 Mathematica, 有利于直接符号运算以得到方程.

实际上, Mathematica 已经有了非常丰富的函数来处理刚体, 比如函数 MomentOfInertia 可以直接符号求得几何区域的惯量张量, 函数 EulerMatrix 可以生成以任意方式定义的 Euler 角类的旋转所产生的旋转矩阵.

这里我们给出如何计算并可视化轮胎面的滚动. 首先定义基本的物理量并给出方程:

At = EulerMatrix[{phi[t], theta[t], psi[t]}, {3, 1, 3}];(*Euler旋转矩阵*)
II = {{i1, 0, 0}, {0, i1, 0}, {0, 0, i3}};(*惯性张量*)
Omega = {phi'[t] Sin[theta[t]] Sin[psi[t]] + theta'[t] Cos[psi[t]], 
   phi'[t] Sin[theta[t]] Cos[psi[t]] - theta'[t] Sin[psi[t]], 
   phi'[t] Cos[theta[t]] + psi'[t]};
omega = At . Omega // Simplify;
gamma = {R Cos[theta[t]] Sin[phi[t]], -R Cos[theta[t]] Cos[
     phi[t]], -r - R Sin[theta[t]]};
pp[{theta_, 
    phi_}] := {R Cos[theta] Sin[phi], -R Cos[theta] Cos[phi], -r - 
    R Sin[theta]};
n = {0, 0, 1};
preeq = At . (Cross[Omega, II . Omega] + II . D[Omega, t]) - 
   Cross[gamma, m g n - m D[Cross[omega, gamma], t]];

我们想要使得质心的初始速度为 0, 为此可以符号求解一下角速度应该满足的关系:

Clear[R, r]; Quiet@
 Solve[-Cross[omega, gamma] == {0, 0, 0}, {phi'[t], theta'[t], 
   psi'[t]}]

我们得到:

{{Derivative[1][phi][
    t] -> -(((R Cos[theta[t]] + r Tan[theta[t]] + 
       R Sin[theta[t]] Tan[theta[t]]) Derivative[1][psi][t])/R), 
  Derivative[1][theta][t] -> 0}}

下面给出具体参数, 并给出初值, 数值求解微分方程:

i1 = 1; i3 = 10; R = 2; r = 1;
m = 20; g = 10;
eqgen[f_] := Table[f[[i]] == 0, {i, 1, Length@f}];
eq = eqgen[preeq];
mydphi[theta_, 
   dpsi_] := -(((R Cos[theta] + r Tan[theta] + 
      R Sin[theta] Tan[theta]) dpsi)/R);
phi0 = Pi/4; theta0 = Pi/4; psi0 = 
 Pi/4; dtheta0 = 0; dpsi0 = 1.2; dphi0 = mydphi[theta0, dpsi0];
initials = {phi[0] == phi0, theta[0] == theta0, psi[0] == psi0, 
   theta'[0] == dtheta0, phi'[0] == dphi0, psi'[0] == dpsi0};
(*Euler 角满足的方程求解*)
sol = NDSolve[Join[eq, initials], {phi, theta, psi}, {t, 0, 100}, 
    SolveDelayed -> True][[1]];
(*质心运动方程求解*)
sol2 = NDSolve[{q'[t] == -Cross[omega, gamma] /. sol, 
     q[0] == {0, 0, 0}}, q, {t, 0, 100}][[1]];

最后可视化:

floor = (gamma /. sol /. t -> 10) + ((q[t]) /. sol2 /. 
     t -> 10);(*盘所在的平面*)
rotate[t_] = EulerMatrix[{phi[t], theta[t], psi[t]}, {3, 1, 3}] /. sol;
translate[t_] = q[t] /. sol2;
contact[t_] := (pp[{theta[t], phi[t]}] /. sol) + ((q[t]) /. sol2);
R = 2; r = 1;
f[a_, b_] := {(R + r Cos[b]) Cos[a], (R + r Cos[b]) Sin[a], 
   r Sin[b]};
fig = ParametricPlot3D[f[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi}, 
   PlotStyle -> 
    Directive[Specularity[White, 30], 
     Texture[ExampleData[{"ColorTexture", "StoneWall"}]]], 
   Lighting -> "Standard", Mesh -> None, PlotRange -> All];
Animate[Show[
  fig /. 
   GraphicsComplex[x___] :> 
    GeometricTransformation[
     GeometricTransformation[GraphicsComplex[x], rotate[t]], 
     TranslationTransform[translate[t]]], 
  Graphics3D[{LightPink, InfinitePlane[floor, {{1, 0, 0}, {0, 1, 0}}],
     Red, PointSize[0.02], Point[contact[t]]}], 
  PlotRange -> {{-8, 8}, {-8, 8}, {-4, 4}}, 
  ImageSize -> {400, 400}], {t, 0, 50}]

由于 Gitee 不支持视频播放及预览, 读者可以点击这里下载视频.

最后我们画出接触点的轨迹:

ParametricPlot[contact[t][[1 ;; 2]], {t, 0, 100}, PlotPoints -> 2000, 
 PlotStyle -> {Black}, Axes -> False, Frame -> True, 
 LabelStyle -> 
  Directive[Black, {FontFamily -> "Times New Roman", 18}]]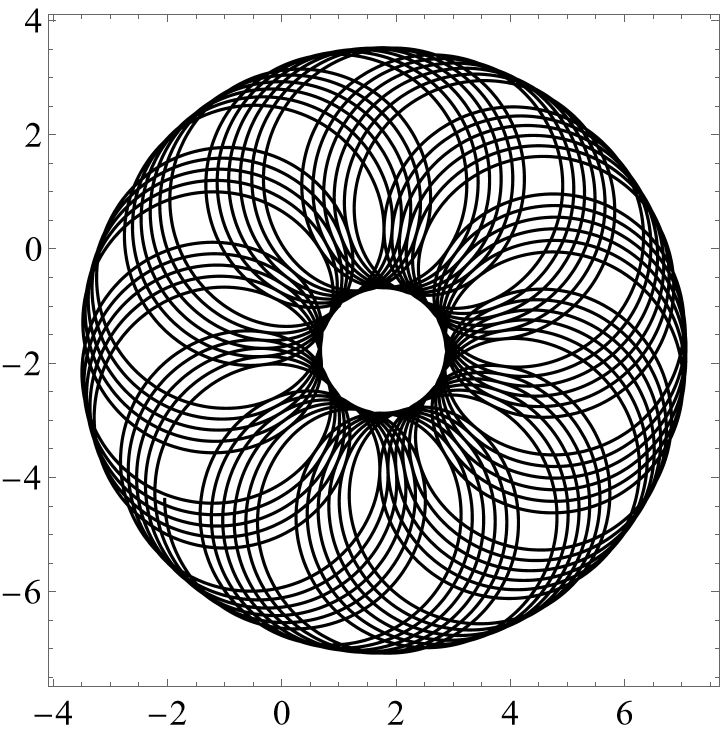

接触点轨迹

参考文献

  • D. Petrie, J. L. Hunt, and C. G. Gray. Does the Euler Disk slip during its motion?. American Journal of Physics, 70:1025–1028, 2002.

Website built with Franklin.jl and Julia.